3.2.2 Simplify

Simplification is the most frequently applied transformation. The subject determines which of three modes of simplification will be used. One mode, called fundamental simplification, performs the operation associated with the operator if the operands are manifest. Another mode, called algebraic simplification, consists of many different but rather trivial transformations based on the algebra associated with the operand types. Together, these two modes are also called non-specific simplification. The third mode, called specific simplification, is triggered when the subject is a designated mathematical construct.

3.2.2.1 Algebraic simplification

Non-specific (or algebraic) simplification is in effect when there is no explicit selection or where the selection fails the candidacy test for special simplification. In this mode, the subject is subdivided into many small subexpressions that are each subjected in turn to algebraic simplification before their containing expression is simplified. In computer-science terms, the simplification algorithm performs a postfix traversal of the expression tree, applying simplification to each operator after simplifying its operands.

In general terms, given two expressions with different forms and the same algebraic meaning, one is simpler than the other if it contains fewer operands, fewer variables or operators with reduced strength. For example, x+x+x simplifies to 3⋅x, which contains both fewer operators and fewer variables. 2⋅x is simpler than x+x because, even though addition is weaker than multiplication, the former expression contains only one occurrence of a variable.

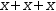
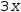
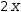
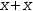
Here are the kinds of transformations that are performed during non-specific simplification.

Constant collection.

Constant operands of multiplicative binary operators are reordered to the left. Constant operands of additive binary operators are reordered to the right. When two of three operands of compatible commutative binary operators are constants, they are reordered with constants to the left (for multiplicative operators) or right (for additive operators) so that constant folding can be applied. 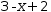For example, 3-x+2 simplifies via an intermediate step to -x+3+2 and then to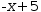 -x+5;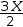 3⋅X÷2 simplifies to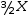 3/2⋅X.

Constant folding.

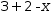
When both operands of an operator meet the fundamental criteria, the operator is replaced with the fundamental simplification provided by the operator. For example, 3+2-x simplifies to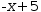 -x+5 and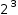 2^3 simplifies to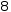 8.

Constant factoring.

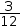
When both operands of a divide operator are integer values, the expression is reduced by removing common integer factors. For example, 3÷12 simplifies to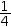 1÷4 and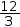 12÷3 simplifies to 4. Non integer values are never introduced by simplification. If they are required, use Evaluate .

Rectification.

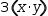
Compatible operators that are out of natural order are rearranged to left-to-right order. For example, 3⋅(x⋅y) rectifies to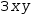 3⋅x⋅y.

Operator reduction.

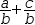
Higher-order operators within lower-order operators can sometimes be combined, resulting in an expression with fewer operators. For example, a÷b+c÷b simplifies to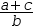 (a+c)÷b and a^b⋅a^c simplifies to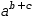 a^(b+c)

3.2.2.2 Specific Simplification

Specific simplification, also called special simplification because it is easier to enunciate, is triggered when there is an explicit selection that meets additional criteria. If the selection fails the candidacy test, non-specific simplification is applied but it is restricted to the selection.

The way to think about specific simplification is like an “apply” action. Using integration as an example, an integral expression is a candidate for special simplification. The actual application of integration is not performed during non-specific simplification because the integrand is often a complex expression that must be subjected to many transformations, including simplification, before it is ready for integration. However, if the integral is selected, it becomes a candidate for special simplification. That is, when Simplify is applied to an integral subject, special simplification is performed and the integral expression responds by applying symbolic integration.

Continuing with integration as an example, consider ∫x+x ⅆx in various ways to illustrate the difference between algebraic simplification and special simplification. Without any selection at all, Simplify finds the x+x in the integrand and simplifies it to 2⋅x. The integrand is a simple add expression which is not a candidate for specific simplification. Now consider simplification of ∫.{x+x} ⅆx. Because there is a subject and because the subject is not a candidate for special simplification, Simplify also performs algebraic simplification but just to the subject. If the integral is embedded in a larger expression, like x+x+∫.{x+x} ⅆx, algebraic simplification is confined to the subject. However, if the subject is the entire integral, Simplify performs integration.

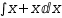
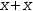
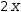
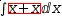
Given an expression with a selected subject, how does Myron choose between specific and non-specific simplification? Refer to Figure §3.1, which enumerates candidates for specific simplification and indicates the transformation.

Expression	Value	Transformation
numeric	simple decimal fractions	integer fractions
	decimal fractions representing a portion of π	fraction with π
	decimal fraction representing Euler's number	ⅇ
	non-integer real	division with integers
exponentiation	negative exponand with fractional exponent	complex
log	base ⅇ	ln x
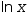trig	constant argument	evaluate
matrix	duplicate trailing rows	reduce
matrix gen	constant template	reduce
set	with duplicates	remove duplicates
	with pair having opposite signs	complex
	any elements	randomize order
tuple	duplicate trailing elements	reduce
tuple gen	constant template	reduce
derivative	suitable derivand	derive
partial	suitable derivand	derive
integral	suitable integrand	integrate
integration	with bounds	apply bounds
	with u-decoration	substitute decoration
function	in LaPlace notation	Leibnitz notation
	as derivand	LaPlace notation
piecewise	nested piecewise	combine choices
product series	constant bounds and independent template	exponentiation
sum series	constant bounds and powers of n	sum formula
±,∓	as unary operator	set with opposite signs